Q:BN解决了什么问题?
解决两个问题:
- Internal Covariate Shift:深度神经网络涉及到很多层的叠加,而每一层的参数更新会导致上层的输入数据分布发生变化,通过层层叠加,高层的输入分布变化会非常剧烈,这就使得高层需要不断去重新适应底层的参数更新。
- 梯度消失:由于之前Sigmoid一类的激活函数的存在,数据在网络中传播时整体分布逐渐往非线性函数的取值区间的上下限两端靠近,导致反向传播时低层神经网络的梯度消失,神经网络收敛变慢。
Q:BN的运作方式
通过一定的规范化手段,把每层神经网络任意神经元输入值的分布强行拉回到均值为0方差为1的标准正态分布。让梯度变大,避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。同时固定该层的输入分布,使后一层的神经元不用反复重新适应分布的变化。
但经过这一步后大部分值落入激活函数的线性区内,使得激活函数失去了其本身的非线性意义,网络表达能力下降。所以BN为了保证非线性的获得,对变换后的满足均值为0方差为1的x又进行了缩放平移操作(y=scale*x+shift)。核心思想应该是想找到一个线性和非线性的较好平衡点,既能享受非线性的较强表达能力的好处,又避免太靠非线性区两头使得网络收敛速度太慢。
Q:手撕BN
BatchNorm2D(常用于卷积神经网络)
1 | import numpy as np |
BatchNorm1D大概也能根据以上代码进行修改(我瞎写的,仅供参考)
1 | class BatchNorm1D(): |
Q:BN能防止过拟合吗?为什么?
BN能一定程度上缓解过拟合。BN使得模型在训练时的输出不仅仅根据当前的输入样本信息,还包含了同一batch其他样本的信息。训练时,同一个样本跟不同的样本组成一个mini-batch,它们的输出是不同的。相当于在神经网络中进行了数据增强。
Q:BN 有哪些参数?
可训练的参数有缩放因子和平移因子,统计参数有均值和方差,超参数有动量,2D的超参数还包含通道数。
Q:BN 的反向传播推导
- [ ] TODO
Q:BN 在训练和测试的区别?
训练时使用的是当前batch的样本统计量进行归一化,测试时使用的是在训练过程中更新迭代计算得到的均值和方差进行归一化。
Q:BN通常放在什么位置?
BN通常放在激活函数前。因为BN的作用本来就是为了调整上一层的输出分布,让激活层更好地使用这些输出值。
Q:BN可以防止过拟合吗?
BN可以一定程度上缓解过拟合。在样本shuffle训练的情况下,某个样本在不同epoch遇到的同一个batch的其他样本都是不一样的,于是会产生不同的均值和标准差,相当于在模型内部做了数据增强。
Q:BN和Dropout同时用会怎样?怎样才能同时使用?
Dropout在训练(或测试)阶段会根据神经元保留率来对神经元权重进行缩放,这会导致测试时隐藏层输出值的方差跟训练时不同。而BN此时已经根据训练数据统计固定了方差参数,无法适应改变后的方差。多层累积下来产生方差偏移,影响模型效果。所以只有在Dropout在所有BN后面时能同时使用。
Q:有什么其它的归一化方法?
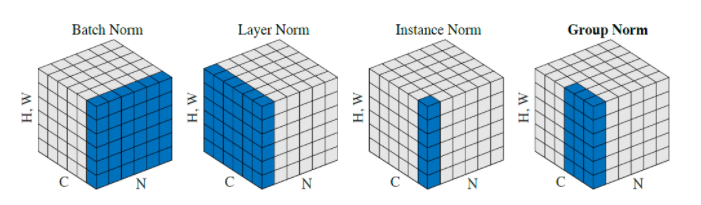
- IN(Instance Norm):实例归一化。与BN的区别在于,BN使用整个batch的统计量作为参数进行归一化,而IN仅使用当前样本的统计量。IN常用于风格迁移任务中。
- AdaIN:自适应的实例归一化。在IN的基础上,将缩放和平移参数分别固定为目标风格图像的标准差和均值。在风格迁移中可以快速适应任意风格。
- LN(Layer Norm):与BN的区别在于,BN是对于一个batch样本的单个通道进行归一化,LN是对单个样本的所有通道进行归一化。可用于RNN或者小batch。
- GN(Group Norm):组归一化。和LN类似,比LN多一个超参数G,G表示分组的数量。同样用来解决在小batch时BN效果较差的问题。