论文地址:Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization
Github:https://github.com/xunhuang1995/AdaIN-style
PyTorch版代码:https://github.com/naoto0804/pytorch-AdaIN
Abstract
Gatys等人最近引入了一种神经算法,可以将一幅内容(Content)图像以另一幅图像的风格(Style)呈现,实现所谓的风格迁移(Style Transfer)。然而,他们的框架需要经历一个缓慢的迭代优化过程,这限制了其实际应用。有人提出用前向神经网络进行快速逼近,以加快神经风格迁移。不幸的是,速度的提高是有代价的:网络通常与一组固定的风格绑定在一起,不能适应任意的新的风格。在本文中,我们提出了一个简单而有效的方法,首次实现了实时任意风格的传输。该方法的核心是一种新的自适应实例归一化(adaptive instance normalization, AdalN)层,它将内容特征的均值和方差与风格特征的均值和方差对齐。我们的方法达到了与现有方法相比最快的速度,并且不受预定义样式集的限制。此外,用户可以灵活调控通过这个方法训练出来的模型,如内容样式权衡、样式插值、颜色和空间控制,所有这些都仅使用一个前向神经网络。

1 Introduction
Gatys等人的开创性工作表明,深度神经网络(DNNs)不仅编码图像的内容,而且编码图像的风格信息。此外,图像风格和内容在某种程度上是可分离的:可以在保留内容的同时改变图像的风格。他们的风格迁移方法足够灵活,可以组合任意图像的内容和样式。但是该方法的优化过程十分缓慢。
在加速神经迁移方向已经有了许多的研究。部分研究试图训练前向神经网络,通过单次前向传递来执行风格化操作。但这些方法限制了每个网络只能训练单一的风格。最近有一些研究解决了这个问题,但它们要么仍然局限于有限的风格集合,要么比单一风格的传输方法慢得多。
在这篇论文中中,我们首次提出了能够解决速度与灵活性矛盾的风格迁移算法。我们的方法可以实时对任意新的风格进行迁移,将基于优化框架的灵活性和前向方法的速度结合在一起。我们的方法灵感来源于实例归一化(instance normalization, IN)层,其在前向风格迁移中非常有效。IN通过对特征统计(feature statistics)进行归一化来进行风格归一化,有些研究表明特征统计携带了图像的风格信息。根据这个解释,我们引入了一个简单的IN扩展,即自适应实例归一化(AdaIN)。对于一组内容和风格,AdaIN只需调整内容输入的平均值和方差,就能匹配风格输入的平均值和方差。通过实验,我们发现AdaIN通过传递特征统计量,有效地将前者的内容与后者的风格结合起来。然后,通过将AdaIN输出反向返回到图像空间,解码网络学会生成最终的风格化图像。在实现了高速风格迁移的同时,我们的方法提供了大量的用户控件,不需要对训练过程进行任何修改。
2 Related Work
Style transfer. 风格迁移问题起源于非真实感渲染,与纹理合成和转换密切相关。早期的一些方法包括线性滤波器响应的直方图匹配和非参数采样。这些方法通常依赖于低级的统计信息,并且常常无法捕获语义结构。Gatys等通过匹配DNN卷积层的特征统计量,首次展示了令人印象深刻的风格迁移结果。最近,许多研究对风格迁移的算法进行了一些改进。Li和Wand在深度特征空间中引入了一种基于马尔可夫随机场的框架来加强局部模式。Gatys等人提出了控制色彩保存、空间位置的方法。以及风格迁移的规模。Ruder等人通过添加时序约束提高了视频风格迁移的质量。
Gatys等人的框架基于一个缓慢的优化过程,迭代更新图像,以最小化由内容损失和样式损失。即使是现代GPU也需要几分钟的时间,而移动应用程序中的设备处理速度更慢,难以实现。一个常见的解决方法是用训练最小化相同目标的前馈神经网络来代替优化过程。这些前馈风格的传输方法比基于优化的替代方法大约快三个数量级,为实时应用打开了大门。Wang等人的使用多分辨率架构增强了前馈式传输的粒度。Ulyanov等人提出了提高生成样本质量和多样性的方法。然而,上述前馈方法的局限性在于,每个网络都被绑在一个固定的样式上。为了解决这个问题,Dumoulin等人引入了一个能够编码32种样式及其插值的单一网络。与我们的工作同时,Li等人提出了一种前馈架构,可以合成多达300种纹理和转移16种风格。但是,上述两种方法不能适应训练中没有观察到的任意风格。
最近,Chen和Schmidt引入了一种前馈方法,借助风格交换层可以传输任意的风格。对于给定内容和风格图像的特征激活,风格交换层将以patch-by-patch的方式将内容特征替换为最匹配的风格特征。然而,他们的风格交换层创造了一个新的计算瓶颈:超过95%的计算花费在512 x 512输入图像的样式交换上。我们的方法允许任意的风格的同时,比他们的方法快1-2个数量级。
风格迁移的另一个核心问题是使用哪种风格损失函数。Gatys等人的原始框架通过匹配Gram矩阵捕获的特征激活之间的二阶统计量来匹配风格。后来也有研究提出了其它的损失函数,如MRF损失,adversarial 损失,直方图损失,CORAL损失,MMD损失,以及信道平均和方差之间的距离。注意,以上所有的损失函数都是为了匹配风格图像和合成图像之间的一些特征统计。
Deep generative image modeling. 有几个图像生成框架可供选择,包括变分自动编码器、自回归模型和生成对抗网络(GANs)。值得注意的是,GANs已经取得了最令人印象深刻的视觉质量。GAN框架的各种改进已经被提出,比如条件生成、多级处理以及更好的训练目标。GANs也被应用于风格迁移和跨域图像生成。
3 Background
3.1 Batch Normalization
loffe和Szegedy的开创性地引入了批归一化(BN)层,通过对特征统计进行归一化,显著地简化了前馈网络的训练。BN层的设计初衷是为了加速识别网络的训练,但后来被发现在生成图像模型中也是有效的。对于给定批处理输入x,BN对每个特征通道的均值和标准差进行归一化:
其中$\gamma$和$\beta$从数据中习得,$\mu(x)$和$\sigma$是batch的均值和标准差,由每个特征通道的batch size和空间维度独立计算而得:
BN在训练时使用mini-batch统计,在推理时使用常规的统计代替,造成了训练和推理的差异。为了解决这个问题,最近提出了批重正化,在训练期间逐步使用常规的统计数据。Li等人发现BN的另一个有趣应用:BN可以通过重新计算目标域的常规统计数据来减轻域偏移。
3.2 Instance Normalization
在原始的前馈风格化方法中,风格迁移网络在每个卷积层之后包含一个BN层。令人惊讶的是,Ulyanov等发现,只需将BN层替换为IN层,就可以得到显著的改善:
和BN不同的是,IN的的$\mu(x)$和$\sigma(x)$是对每个通道和每个样本独立计算的:
另一个区别是,在测试时应用的层不变,而BN层通常使用常规统计代替mini-batch统计。
3.3 Conditional Instance Normalization
Dumoulin等人没有学习单一的仿射参数集$\gamma$和$\beta$,而是提出了条件实例归一化(CIN)层,该层对每种不同的风格$s$学习不同的参数集$\gamma^s$和$\beta^s$:
在训练过程中,从一组固定的风格集合$s\in {1,2,…,S}$(实验中$S = 32$)中随机选取一幅风格图像及其索引$s$。然后将内容图像输入到一个网络中,在CIN层使用对应的$\gamma^s$和$\beta^s$。令人惊讶的是,有着相同卷积参数、不同仿射参数的多个网络,可以生成完全不同风格的图像。
与没有归一化层的网络相比,有CIN层的网络需要增加$2FS$的附加参数,其中$F$为网络中feature map的数量。由于附加参数的数量与样式的数量成线性关系,因此很难用这个方法生成非常多的风格。而且,每添加一种新的风格,都需要重新训练一次网络。
4 Interpreting Instance Normalization
尽管IN取得了巨大的成功,但它们对样式转换起作用的原因仍然是难以捉摸的。Ulyanov等人把IN的成功归于其内容图像的不变性。然而,IN发生在特征空间中,因此它应该比在像素空间中进行简单的对比归一化具有更深远的影响。也许更令人惊讶的是IN中的仿射参数可以完全改变输出图像的风格。
众所周知,DNN的卷积特征统计可以捕捉到图像的风格。Gatys等人使用二阶统计量作为其优化目标,而Li等人最近表明,包括channel-wise的均值和方差在内的其它统计量对风格迁移也是有效的。因此我们认为IN通过归一化特征统计(即均值和方差),在某种程度上执行了“风格归一化(style normalization)”。于是我们认为网络的特征统计也可以控制生成图像的风格。
我们分别运行带有IN和BN层的网络来执行单一风格的转换。正如预期的那样,使用IN的模型比BN模型收敛得更快(如下图)。为了检验Ulyanov的解释,我们通过对亮度通道进行直方图均衡化,将所有训练图像归一化到相同对比度。如图(b)所示,IN仍然有效,说明Ulyanov的解释不完全。为了验证我们的假设,我们使用预训练的风格转移网络将所有的训练图像归一化为相同的风格(不同于目标风格)。从图(c)可以看出,在对图像进行了风格归一化后,IN带来的改进就小得多了。另外,使用风格归一化图像训练BN的模型和使用原始图像训练IN的模型收敛速度一样快,表明IN确实执行了一种风格归一化。
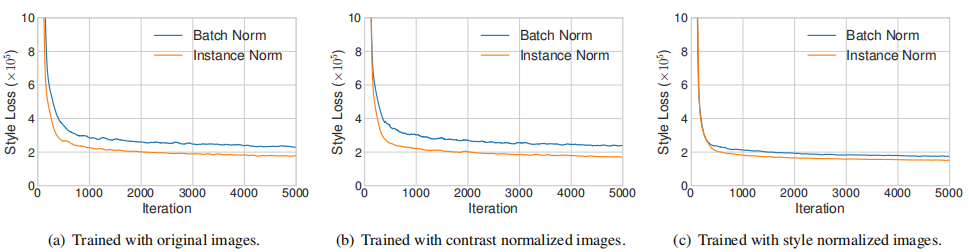
由于BN是在一个batch的样本上进行特征统计,可以直观地理解为将一个batch的样本围绕着单一风格进行归一化。然而每一个的样本都有不同的风格,很难将一个batch中所有样本转化成同一个风格。虽然卷积层可能会学会弥补样本之间风格的差异,但也为训练增加了难度。另一方面,IN可以将每个样本的风格归一化为目标风格,网络的其他部分可以在舍弃原有信息风格的同时专注于内容处理,提高了训练速度。CIN成功的原因也很明确:不同的仿射参数可以将特征统计值归一化到不同的值,从而将输出的图像归一化到不同的风格。
5 Adaptive Instance Normalization
如果将输入归一化为由仿射参数指定的单一风格,是否有可能通过自适应仿射变换使其适应任意给定的风格?我们对IN进行了一个简单的扩展。我们称之为自适应实例归一化(AdaIN)。AdaIN接收一个内容输入x和一个样式输入y,并简单地将x的通道平均值和方差与y的平均值和方差匹配。与BN、IN和CIN不同,AdaIN没有可以学习的仿射参数。相反,它自适应地从风格输入中计算仿射参数:
相比于IN,我们仅仅是将两个仿射参数替换成了$\sigma (y)$和$\mu (y)$,这两个统计值的依然是在空间位置上进行计算。
假设存在一个检测特定风格纹路的特征通道。具有这种纹路的风格图像将在该层产生较高的平均激活值。AdaIN产生的输出在保持内容图像的空间结构的同时,对该特征具有同样高的平均激活度。纹路特征可以通过前馈解码器转换到到图像空间。该特征通道的方差可以将更细微的风格信息传递到AdaIN输出和最终输出的图像中。
简而言之,AdaIN通过迁移特征统计量,即通道方向上的均值和方差,在特征空间中进行风格迁移。
6 Experimental Setup
如下是我们基于AdaIN的风格迁移网络的概览图:
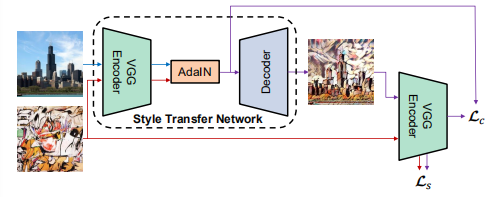
6.1 Architecture
我们的风格迁移网络$T$以一个内容图像$c$和一个任意风格的图像$s$作为输入,并合成一个输出图像,该图像重新组合前者的内容和后者的样式。我们采用一种简单的encoder-decoder架构,其中encoder $f$ 固定在预训练VGG-19的前几层(直到relu4_1)。在特征空间中对内容和风格图像进行编码后,我们将这两种特征图输入AdalN层,使内容特征图的均值和方差与风格特征图的均值和方差对齐,生成目标特征图$t$:
训练一个随机初始化的decoder $g$将$t$映射回图像空间,生成风格化图像$T (c, s)$:
decoder大部分是encoder的镜像,所有池化层替换为最近的上采样,以减少棋盘效应。我们在$f$和$g$中使用反射填充((reflflection padding)来避免边界失真。另一个问题是decoder应该使用IN、BN还是不使用标准化层。如第4节所述,IN将每个样本归为单个样式,而BN将一批样本归一化,以单个样式为中心。当我们希望decoder生成风格迥异的图像时,两者都是不可取的。因此,我们在decoder中不使用归一化层。
6.2 Training
- Dataset
- Content: MS-COCO
- Style: WikiArt
- Sample size: 80000
- Optimizer: adam
- Batch size: 8 content-style image pairs
- Resize: 512, RandomCrop: 256×256
- Model: VGG-19
- Loss: $L=L_c+\lambda L_s$
损失函数为内容损失和风格损失的加权和。内容损失是目标特征与输出图像特征之间的欧氏距离。我们使用AdaIN输出$t$作为内容目标,而不是内容图像:
由于AdaIN层只迁移了风格特征的平均值和标准差,所以我们的风格损失只与这些统计数据匹配。虽然我们发现常用的Gram矩阵损失可以产生类似的结果,但我们还是使用IN统计,因为它在概念上更清晰。
其中$\phi$表示VGG-19中用于计算风格损失的层。在我们的实验中,我们在relu1_1, relu2_1, relu3_1, relu4_1中使用了相等的权重。